schoolsraka.blogg.se

1. #Capital asset pricing model full
2. #Capital asset pricing model code

So, not altogether unexpectedly, it seems that the market risk premium

The parameter estimate for, the intercept, is not significantly different fromĬoefficient of R_MKT, is 1.05 and is highly significant. The output provides information about the appropriateness of the model chosen. Output out=tandyout p=p r=r ucl=u lcl=l alphacli=.10 In addition, the OUTPUT data set TANDYOUTĬontains the predicted values of R_TANDY, the residuals of the regression, and the upper and lower bounds of the 90% Statement is requesting a test that the coefficient of R_MKT is equal to 1. The TEST statement enables you to perform hypothesis tests on parameter estimates the following TEST The DWPROB option requests the Durbin-Watson test for autocorrelation of In the model unless the NOINT option is specified. Note that a constant term is automatically included The AUTOREG procedure specifies a linear regression of R_TANDY on R_MKT. Based on this visual evidence, a linear model between R_TANDY and R_MKT is not Increases, so should the return of most stocks. This positive relationship seems sensible: as the market return The risk premium of the Tandy Corporation's stock. The plot of the Tandy data set above indicates that there is a positive relationship between the risk premium of the market and Title3'Tandy Corporation versus the Market' Plot r_tandy * r_mkt / haxis=axis1 hminor=4 cframe=ligrĪxis2 label=(angle=90 'Tandy Corp. Premium of the Tandy Corporation against the risk premium of the Market.

#Capital asset pricing model code

The following code uses the GPLOT procedure to plot the risk A simple plot allows for a visualĪssessment of the appropriateness of the proposed model. It is always a good idea to look at the data to be sure that it was input as expected. R_tandy='Risk Premium for Tandy Corporation' Tandy='Rate of Return for Tandy Corporation' Return that investors require for bearing risk. A risk premium is the excess return of a security over the risk-free rate or, rather, the extra Two new variables, R_TANDY = TANDY - R_F and R_MKT = R_M - R_F, that correspond to the risk premiums for the TandyĬorporation and the Market. Using a SAS DATA step, enter the data and create Risk-free rate, and the return on the Tandy Corporation's common stock. The data for this example consist of monthly observations from January 1978 through December 1987 on the market return, the S&P 500 or the Dow Jones Industrial Average), the risk-free rate of return (usually a short-term Treasury bill), and stock The CAPM relates the sensitivity of an individual company's stock returns to the returns of the market as a whole.Įstimating a model for a particular firm requires data on the market rate of return (typically a composite index such as the This example uses stock returns from the Tandy Corporation to estimate a CAPM and perform some general tests of the model. Particular company is the same as that of the market as a whole. Failure to reject would imply that the movement of asset prices of a The alternative that it is not equal to 1. A rejection would cast some doubt on the theoretical model as is assumed to be 0 in the first Two straightforward tests of this model areĪgainst the alternative that it is not equal to 0. There are, however, several econometric issues involved in the more general modelĭisturbance term with mean zero and variance.

#Capital asset pricing model full

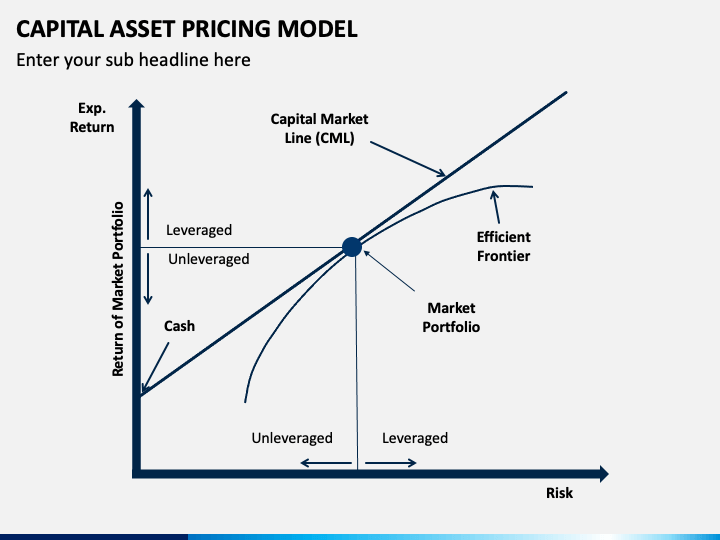
The term is the ratio of the standard deviations of returns on security j to the market.Ī full development of the CAPM can be found in any introductory finance textbook (for example, Brealey and Myers 1988), and

Risk-free asset and the market return, respectively. Specifically, the CAPM linear relationship can be written as The Capital Asset Pricing Model (CAPM) is one of the most common methods of relating the sensitivity of an individualĬompany's stock return to the return of the market as a whole.